马修·伯恩斯坦讲线性代数系列：矩阵-向量乘法

原文: Matrix-vector multiplication

引言

在上一篇博客文章中，我们讨论了观察矩阵的三种方式：作为值表格、作为向量列表，以及最终作为函数。正是第三种观察矩阵的方式赋予了矩阵真正的力量。在这里，我们将介绍矩阵和向量之间的一种操作，称为矩阵-向量乘法，这将使我们能够将矩阵用作函数。

矩阵-向量乘法是矩阵和向量之间的一种操作，会产生一个新向量。值得注意的是，矩阵-向量乘法仅定义在矩阵和向量之间，其中向量的长度等于矩阵的列数。其定义如下：

定义 1 (矩阵-向量乘法)： 给定矩阵 \(\boldsymbol{A} \in \mathbb{R}^{m \times n}\) 和向量 \(\boldsymbol{x} \in \mathbb{R}^n\)，\(\boldsymbol{A}\) 和 \(\boldsymbol{x}\) 的矩阵-向量乘法定义为

\[\boldsymbol{A}\boldsymbol{x} := x_1\boldsymbol{a}_{*,1} + x_2\boldsymbol{a}_{*,2} + \dots + x_n\boldsymbol{a}_{*,n}\]

其中 \(\boldsymbol{a}_{*,i}\) 是 \(\boldsymbol{A}\) 的第 \(i\) 个列向量。

像大多数数学概念一样，矩阵-向量乘法可以从多个角度审视，具有不同程度的抽象性。这些视角在尝试概念化我们利用矩阵-向量乘法来建模现实世界问题时的各种方式时非常有用。以下是我发现用于概念化矩阵-向量乘法的三种方式，按从最不抽象到最抽象排序：

1. 作为一种“逐行”的向量生成过程： 矩阵-向量乘法定义了一个使用现有向量创建新向量的过程，其中新向量的每个元素是通过使用向量元素作为系数，对矩阵的每一行取加权和而“生成”的。
2. 作为矩阵列的线性组合： 矩阵-向量乘法是使用向量元素作为系数，对矩阵的列空间取线性组合的过程。
3. 作为向量空间之间函数的求值： 矩阵-向量乘法允许矩阵定义两个向量空间之间的映射。

我发现所有三种视角都很有用。前两种视角提供了理解矩阵-向量乘法机制的方式，而第三种视角提供了矩阵-向量乘法的本质。正是这种矩阵-向量乘法的第三种视角使我们能够将矩阵视为函数，正如我们在上一篇中讨论的那样。

矩阵-向量乘法作为一种“逐行”的向量生成过程

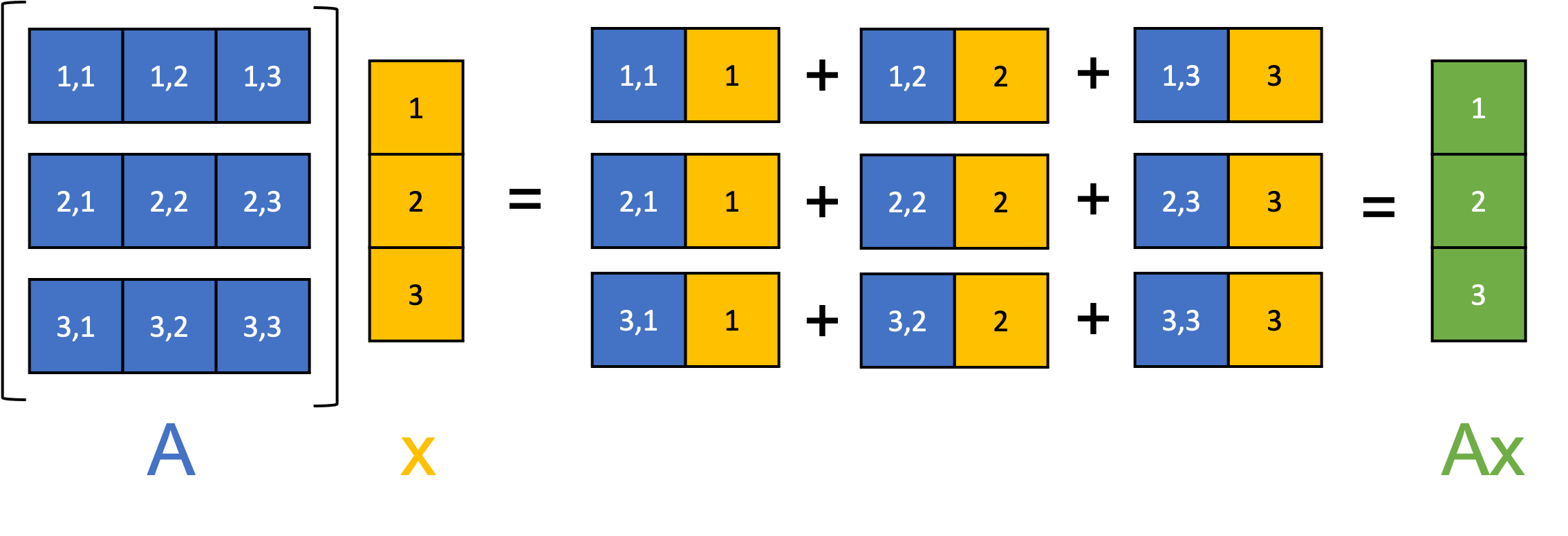
审视矩阵 \(\boldsymbol{A}\) 和向量 \(\boldsymbol{x}\) 之间矩阵-向量乘法的机制的一种有用方式是将它视为一种“过程”（甚至可以视为计算机程序），它以迭代方式构建输出向量的每个元素，其中我们迭代 \(\boldsymbol{A}\) 的每一行。具体来说，对于 \(\boldsymbol{A}\) 的每一行 \(i\)，我们取 \(\boldsymbol{x}\) 并计算 \(\boldsymbol{x}\) 与矩阵第 \(i\) 行的点积，从而产生输出向量的第 \(i\) 个元素（参见本文附录中的定理 1）：

\[\boldsymbol{Ax} = \begin{bmatrix} \boldsymbol{a}_{1,*} \cdot \boldsymbol{x} \\ \boldsymbol{a}_{2,*} \cdot \boldsymbol{x} \\ \vdots \\ \boldsymbol{a}_{m,*} \cdot \boldsymbol{x} \\ \end{bmatrix}\]

其中 \(\boldsymbol{a}_{i,*}\) 是 \(\boldsymbol{A}\) 中的第 \(i\) 个行向量。这个过程在下面的图中示意性地说明：

矩阵-向量乘法作为矩阵列的线性组合

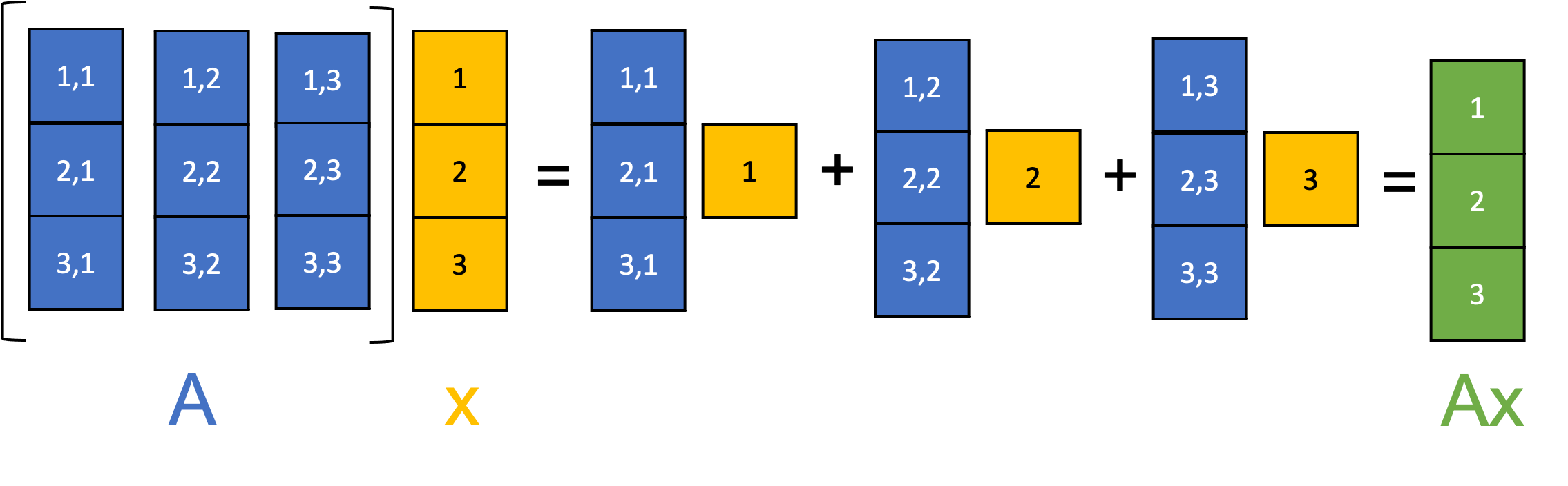
\(\boldsymbol{A} \in \mathbb{R}^{m \times n}\) 和 \(\boldsymbol{x} \in \mathbb{R}^n\) 之间的矩阵-向量乘法可以理解为使用 \(\boldsymbol{x}\) 的元素作为系数，对 \(\boldsymbol{A}\) 的列向量取线性组合。这个过程在下面的示意图中说明：

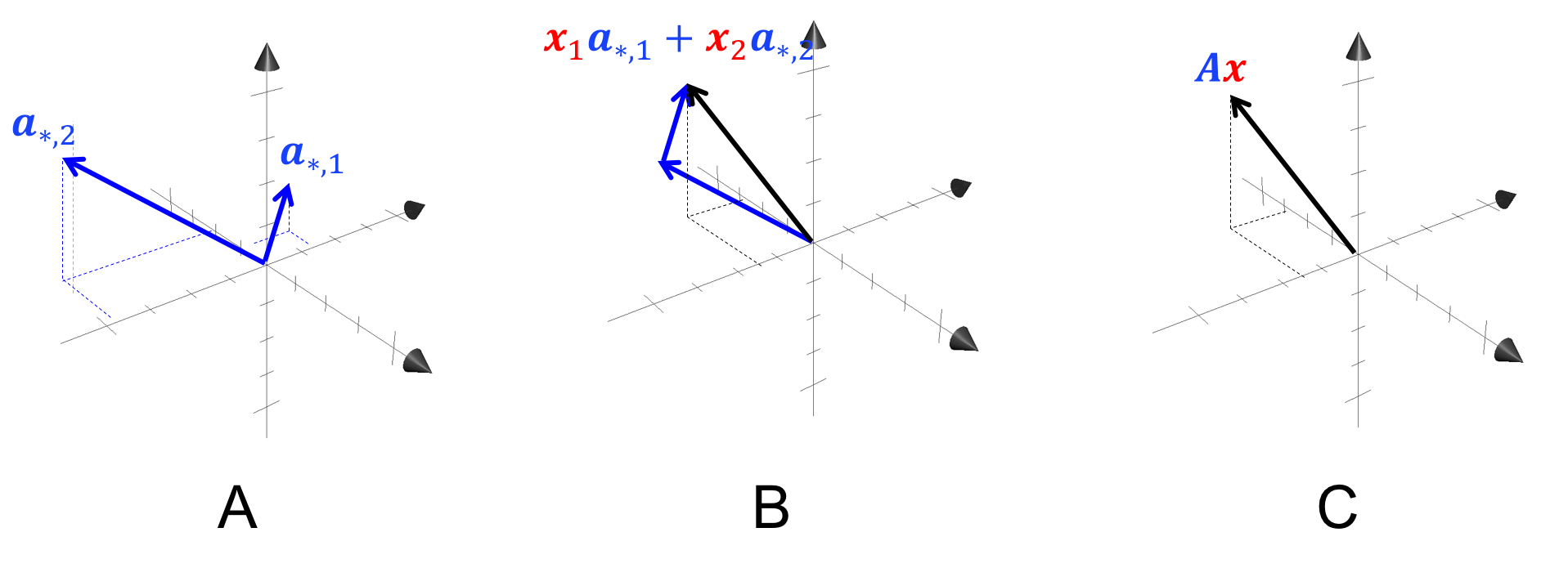
我们也可以从几何角度审视这个过程：

在面板 A 中，我们描绘了某个矩阵 \(\boldsymbol{A} \in \mathbb{R}^{3,2}\) 的两个列向量。在面板 B 中，我们根据某个向量 \(\boldsymbol{x}\) 的元素对 \(\boldsymbol{A}\) 的两个列向量取线性组合，从而产生向量 \(\boldsymbol{Ax}\)（黑色向量），如面板 C 所示。

矩阵-向量乘法作为向量空间之间函数的求值

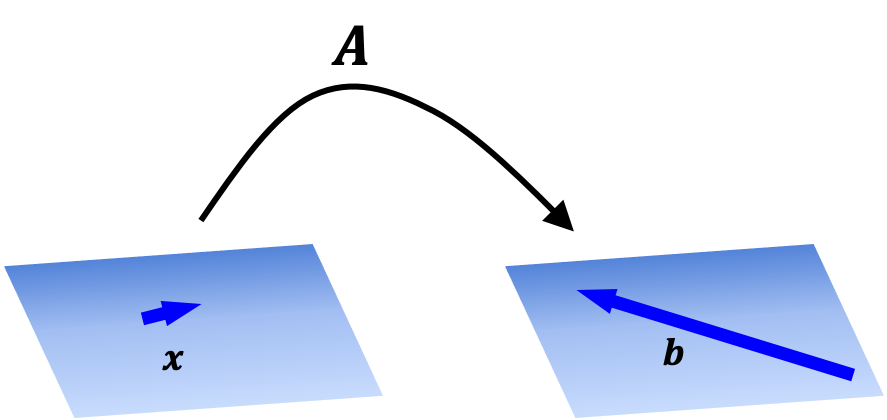
如果我们将矩阵 \(\boldsymbol{A} \in \mathbb{R}^{m \times n}\) 固定，这个矩阵将 \(\mathbb{R}^n\) 中的向量映射到 \(\mathbb{R}^m\) 中的向量。更明确地说，我们可以定义一个函数 \(T : \mathbb{R}^n \rightarrow \mathbb{R}^m\) 为：\(T(\boldsymbol{x}) := \boldsymbol{Ax}\)，其中 \(T\) 使用矩阵 \(\boldsymbol{A}\) 执行映射。

这个过程在下面的示意图中说明：

事实上，正如我们在后续文章中所示，这种由矩阵定义的函数是一种线性函数。更重要的是，任何在有限维向量空间之间定义的线性函数都可以由某个矩阵唯一定义。

附录

定理 1： 给定矩阵 \(\boldsymbol{A} \in \mathbb{R}^{m \times n}\) 和向量 \(\boldsymbol{x} \in \mathbb{R}^n\)，有

\[\boldsymbol{Ax} = \begin{bmatrix}\boldsymbol{a}_{1,*} \cdot \boldsymbol{x} \\ \boldsymbol{a}_{2,*} \cdot \boldsymbol{x} \\ \vdots \\ \boldsymbol{a}_{m,*} \cdot \boldsymbol{x} \\ \end{bmatrix}\]

其中 \(\boldsymbol{a}_{i,*}\) 是 \(\boldsymbol{A}\) 中的第 \(i\) 个行向量。

证明：

\[\begin{align*} \boldsymbol{A}\boldsymbol{x} &:= x_1\boldsymbol{a}_{*,1} + x_2\boldsymbol{a}_{*,2} + \dots + x_n\boldsymbol{a}_{*,n} \\ &= x_1 \begin{bmatrix}a_{1,1} \\ a_{2,1} \\ \vdots \\ a_{m, 1} \end{bmatrix} + x_2\begin{bmatrix}a_{1,2} \\ a_{2,2} \\ \vdots \\ a_{m, 2} \end{bmatrix} + \dots + x_n\begin{bmatrix}a_{1,n} \\ a_{2,n} \\ \vdots \\ a_{m, n} \end{bmatrix} \\ &= \begin{bmatrix}x_1a_{1,1} \\ x_1a_{2,1} \\ \vdots \\ x_1a_{m, 1} \end{bmatrix} + \begin{bmatrix}x_2a_{1,2} \\ x_2a_{2,2} \\ \vdots \\ x_2a_{m, 2} \end{bmatrix} + \dots + \begin{bmatrix}x_na_{1,n} \\ x_na_{2,n} \\ \vdots \\ x_na_{m, n} \end{bmatrix} \\ &= \begin{bmatrix} x_1a_{1,1} + x_2a_{1,2} + \dots + x_na_{1,n} \\ x_1a_{2,1} + x_2a_{2,2} + \dots + x_na_{2,n} \\ \vdots \\ x_1a_{m,1} + x_2a_{m,2} + \dots + x_na_{m,n} \\ \end{bmatrix} \\ &= \begin{bmatrix} \sum_{i=1}^n a_{1,i}x_i \\ \sum_{i=1}^n a_{2,i}x_i \\ \vdots \\ \sum_{i=1}^n a_{m,i}x_i \\ \end{bmatrix} \\ &= \begin{bmatrix}\boldsymbol{a}_{1,*} \cdot \boldsymbol{x} \\ \boldsymbol{a}_{2,*} \cdot \boldsymbol{x} \\ \vdots \\ \boldsymbol{a}_{m,*} \cdot \boldsymbol{x} \\ \end{bmatrix}\end{align*}\]

评论