马修·伯恩斯坦讲线性代数系列：矩阵的介绍

在这里，我将介绍思考矩阵的三种主要方法。当我在本科线性代数课程中第一次接触到矩阵时，这种对矩阵多方面思考方式的高级描述将帮助我更好地直觉矩阵。

引言¶

矩阵是线性代数中的基本概念，在科学和工程领域中无处不在。从表面上看，矩阵只是一个二维的值数组。例如，以下是一个矩阵：

\[\begin{bmatrix}1 & -2 & 0 \\ 4 & -3 & 1 \\ 0 & 6 & -2 \end{bmatrix}\]

正如我在上一篇博客文章中讨论的那样，有些概念需要从多个角度观察才能掌握其真实本质。尽管矩阵表面上很简单，但我认为矩阵是其中一个概念，并且我相信，如果一开始就提供对矩阵的高层次、多视角概述，以便为未来的线性代数学习提供背景，那么对于我--大学线性代数课程的二年级学生来说，这会对我有所帮助。在这篇文章中，我将介绍查看矩阵的三个主要角度，这对我以前的自己有帮助。

预备知识¶

在介绍观察矩阵的三种角度之前，我将介绍一些符号。首先，一个矩阵是一个矩形的值数组。例如，以下矩阵 \(\boldsymbol{A}\) 有 \(m\) 行和 \(n\) 列：

\[\boldsymbol{A} := \begin{bmatrix} a_{1,1} & a_{1,2} & \dots & a_{1,n} \\ a_{2,1} & a_{2,2} & \dots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & \dots & a_{m,n} \end{bmatrix}\]

行向量和列向量¶

回想一个有限维向量 \(\boldsymbol{x}\) 可以表示为一个有序的值列表 \(x_1, x_2, \dots, x_n\)。我们可以将 \(\boldsymbol{x}\) 视为一个只有一行或一列的矩阵。当将 \(\boldsymbol{x}\) 视为矩阵时，我们可以选择将其水平定向，从而创建一个 \(1 \times n\) 矩阵，或者垂直定向，从而创建一个 \(n \times 1\) 矩阵。如果我们将 \(\boldsymbol{x}\) 水平定向，我们就形成了一个称为行向量的矩阵：

\[\begin{bmatrix} x_{1,1} & x_{1,2} & \dots & x_{1,n} \end{bmatrix}\]

如果我们将 \(\boldsymbol{x}\) 垂直定向，我们就形成了一个称为列向量的矩阵：

\[\begin{bmatrix}x_{1,1} \\ x_{2,1} \\ \vdots \\ x_{n,1} \end{bmatrix}\]

符号¶

以下是讨论矩阵的符号概述：

给定一个集合 \(C\)，我们用 \(C^{m \times n}\) 表示所有具有 \(m\) 行和 \(n\) 列的矩阵的集合，这些矩阵由集合 \(C\) 中的元素组成。
给定一个矩阵 \(\boldsymbol{A} \in C^{m \times n}\)，我们用 \(a_{i,j}\) 表示 \(\boldsymbol{A}\) 的第 \(i\) 行和第 \(j\) 列处的元素。
给定一个矩阵 \(\boldsymbol{A} \in C^{m \times n}\)，我们用 \(\boldsymbol{a}_{i,*}\) 表示 \(\boldsymbol{A}\) 的第 \(i\) 个行向量。
给定一个矩阵 \(\boldsymbol{A} \in C^{m \times n}\)，我们用 \(\boldsymbol{a}_{*,j}\) 表示 \(\boldsymbol{A}\) 的第 \(j\) 个列向量。

观察矩阵的三种视角¶

观察矩阵有三种主要角度。从最不抽象到最抽象，这些角度如下：

作为数据表格： 观察矩阵的最简单且最不抽象的方式是将它视为一个二维的值数组。也就是说，一个表格。
作为向量列表： 稍微抽象一些，矩阵也可以被视为有限维向量空间中的向量集合。
作为函数： 观察矩阵的最抽象方式是将它视为向量空间之间函数的编码。具体来说，矩阵可以用来编码有限维向量空间之间的线性变换。正是这种抽象角度构成了线性代数数学领域核心。

在实际应用中，有些矩阵只需通过上述一种视角来解释；然而，在某些情况下，必须通过所有三种视角来观察矩阵。因此，在实践中使用矩阵往往需要在大脑中在这些三种观察/解释方式之间切换。也就是说，在一个上下文中，将矩阵视为向量集合最有帮助，但在另一个上下文中，将矩阵视为函数更有帮助。

在接下来的部分，我将对这些三种角度提供更多深度。

矩阵作为数据表格¶

矩阵的最简单解释是作为一个二维的值数组。以下是一些例子：

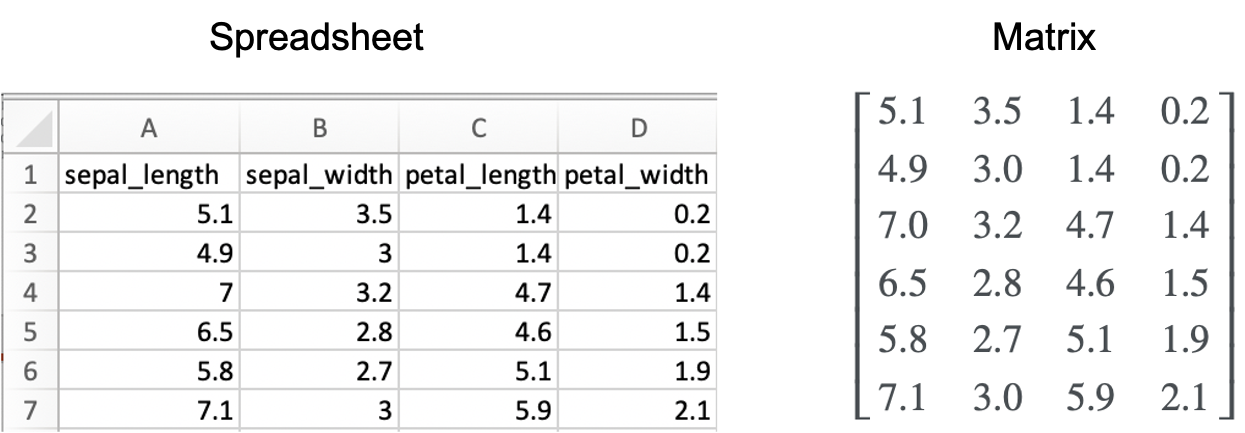
一个数值数据集，例如存储在 Excel 电子表格中的数据，可以表示为一个矩阵。也就是说，列代表不同的字段，行代表不同的条目。例如：
图像的像素可以表示为一个矩阵。假设我们有一个 \(m \times n\) 像素的图像。我们可以让 \(\boldsymbol{X}\) 是一个表示该图像的矩阵，其中 \(x_{i,j}\) 表示第 \(i\) 行和第 \(j\) 列像素的强度。
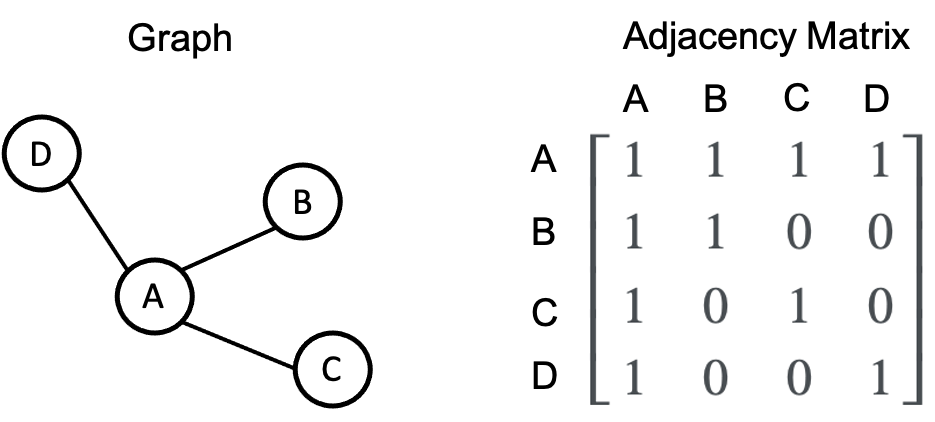
我们可以通过编码哪些节点相互连接来将图表示为一个矩阵。也就是说，如果我们有一个具有 \(n\) 个节点的图，那么我们可以定义一个矩阵 \(\boldsymbol{X} \in \{0, 1\}^{n \times n}\)，使得 \(x_{i,j} = 1\) 如果节点 \(i\) 连接到节点 \(j\)，否则 \(x_{i,j} = 0\)。这称为图的邻接矩阵。例如：

矩阵作为向量集合¶

矩阵可以被视为一组向量。矩阵 \(\boldsymbol{A} \in \mathbb{R}^{m \times n}\) 的第 \(i\) 行，表示为 \(\boldsymbol{a}_{i,*}\)，是 \(\mathbb{R}^n\) 中的一个行向量。该矩阵的第 \(j\) 列，表示为 \(\boldsymbol{a}_{*,j}\)，是 \(\mathbb{R}^m\) 中的一个列向量。

因此，矩阵可以被视为行向量的列表：

\[\boldsymbol{A} := \begin{bmatrix} \boldsymbol{a}_{1,*} \\ \boldsymbol{a}_{2,*} \\ \vdots \\ \boldsymbol{a}_{m,*} \end{bmatrix}\]

或者，作为列向量的列表：

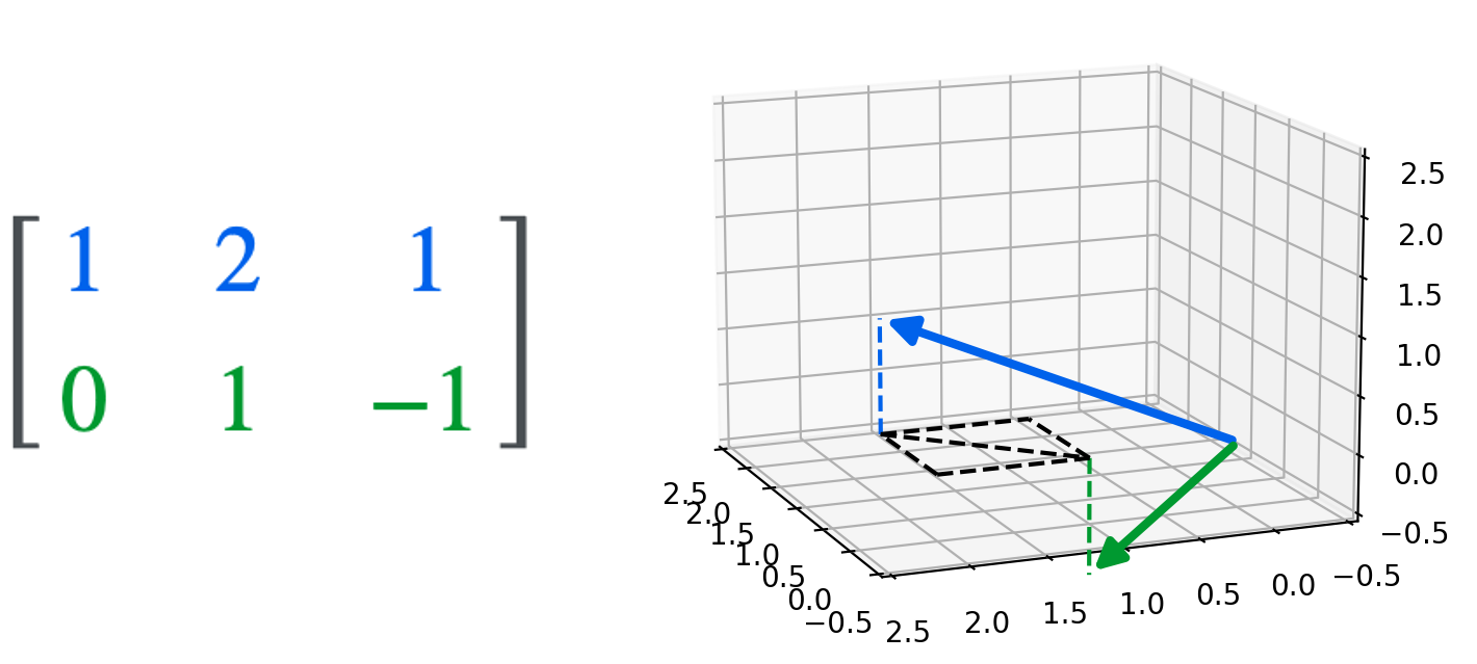
\[\boldsymbol{A} := \begin{bmatrix} \boldsymbol{a}_{*,1} & \boldsymbol{a}_{*,2} & \dots & \boldsymbol{a}_{*,n}\end{bmatrix}\]

例如，以下矩阵

\[\begin{bmatrix}1 & 2 & 1 \\ 0 & 1 & -1\end{bmatrix}\]

可以被视为两个三维行向量（虚线是可视化引导。彩色虚线将每个向量追溯到 \(z = 0\) 平面。黑色虚线描绘了两个向量在 \(z=0\) 平面上的差异）：

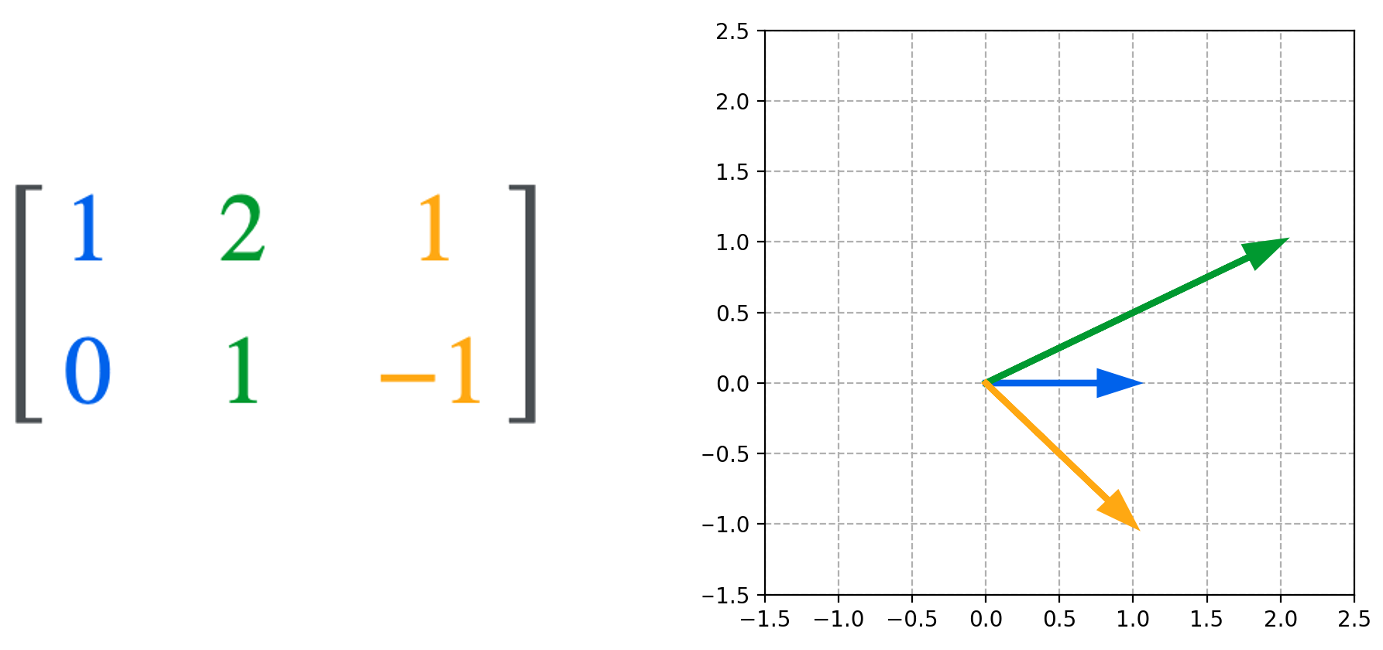
或者，作为三个二维列向量：

矩阵作为向量空间之间的函数¶

矩阵的最抽象且可以说最重要的视角是将它视为一个将一个向量空间中的向量映射到另一个向量空间中的向量的函数。为了将矩阵用作函数，我们首先定义一个矩阵和向量之间的操作，称为矩阵-向量乘法，其中我们将向量乘以矩阵以产生一个新向量：

\[\boldsymbol{Ax} = \boldsymbol{b}\]

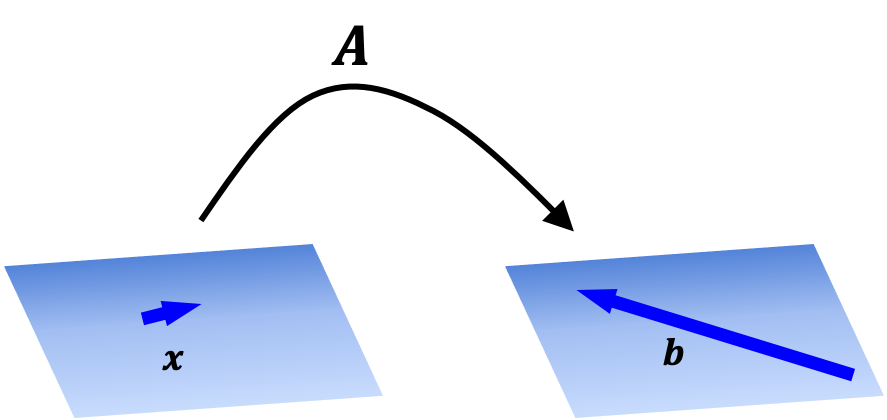
本文不会详细讨论矩阵-向量乘法的定义，但重要的要点是，一旦定义，我们就可以将矩阵视为向量上的函数。也就是说，给定矩阵 \(\boldsymbol{A}\)，我们可以形成一个函数

\[T(\boldsymbol{x}) := \boldsymbol{Ax}\]

这在下面的示意图中描绘：

正如我们将在未来的文章中探讨的，矩阵定义的函数是一种特殊的函数，称为线性变换。事实上，任何在有限维向量空间之间定义的线性变换都可以由一个单一的矩阵来表征，该矩阵执行该变换！因此，我们可以将矩阵视为一个特定的线性变换。