《统计思维》读书笔记之描述性统计量

文章目录

1. 1. 描述性统计量
   1. 1.1. 均值
   2. 1.2. 平均值
      1. 1.2.1. 加权平均值
      2. 1.2.2. 几何平均数
   3. 1.3. 方差
   4. 1.4. 标准差
   5. 1.5. 标准分数
   6. 1.6. 中位数
   7. 1.7. 四分位数
   8. 1.8. 分布
   9. 1.9. 频数
   10. 1.10. 众数
   11. 1.11. 异常值
   12. 1.12. 极差
   13. 1.13. 变异系数
   14. 1.14. 概率质量函数
2. 2. 参考

清明放假三天，闲来无事，拿起角落里吃灰蛮久的《统计思维》一书聊以打发。现把读书笔记结合收集的相关资料内容记录如下。

描述性统计量

描述性统计是一种汇总统计，用于定量描述或总结信息集合的特征。描述性统计又分为集中趋势（Measures of central tendency）和离散趋势（Measures of Dispersion）

均值

均值(Mean)，即所有数据相加后的总和除以数据的个数得出的结果， 也称算术平均值。设一组样本数据为x1,x2,…,xn，样本数据的个数为n，则均值为：

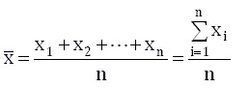
平均值

平均(Average)是若干种可以描述样本的典型值或**集中趋势(central tendency)**的汇总统计量之一。狭义上可以认为平均值就是均值。实际上平均值还有：

加权平均值

计算公式为：

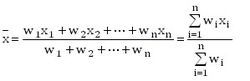
几何平均数

几何平均值是n个变量值乘积的n次方根，用G表示，计算公式为：

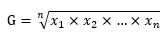
例如一位投资者持有一种股票，连续四年的收益率分别为4.5%,2.1%,25.5%,1.9%，那么该投资者在这四年内的平均收益率为：

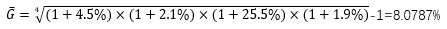
平均值缺点就是对异常值不敏感。一个矮子和姚明在一起计算平均身高，得出来是正常人的身高，没有反应出姚明身高这种”异常“情况。

方差

方差(Variance)描述了分散情况，能够体现异常值情况，计算公式为：

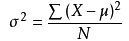
其中u是平均值，X-u叫做离均差(deviation from the mean)。因此方差为该偏差的方均值。

标准差

标准差(Standard deviation)是方差的算术平方根，用σ表示。方差和标准差是用来度量一组数据分散情况的两个数值，但是标准差能更直观地表示出数据中的值与均值的距离。

标准差能反映一个数据集的离散程度，标准偏差越小，这些值偏离平均值就越少，反之亦然。计算公式为：

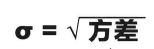
标准分数

标准分数（standard score）也称为Z分数，是一个数与平均数的差再除以标准差的过程。计算公式为：

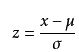
标准分数代表的意义就是某数距离均值的标准差个数。

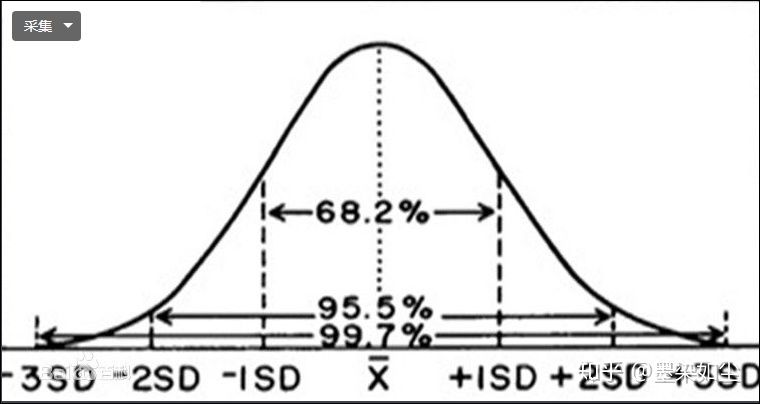
上图中中间虚线表示均值，两条虚线之间的范围表示一个标准差σ

从上图可以发现：

有68.2%的数值位于平均值一个标准差的范围内；

有95.5%的数值位于平均值两个个标准差的范围内；

有99.7%的数值位于平均值三个标准差的范围内。

中位数

中位数(Median)是按顺序排列的一组数据中居于中间位置的数，即在这组数据中，有一半的数据比他大，有一半的数据比他小。

四分位数

四分位数(Inter Quartile Range (IQR))是分位数形式的一种。计算方式是把所有数值由小到大排列并分成四等份，处于三个分割点位置的数值，如图中的Q1、Q2、Q3：

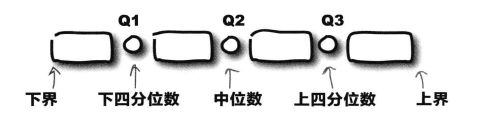
第一四分位数 (Q1)，又称“下四分位数”，等于该样本中所有数值由小到大排列后第 25%的数字。

第二四分位数 (Q2)，又称“中位数”，等于该样本中所有数值由小到大排列后第50%的数字。

第三四分位数 (Q3)，又称“上四分位数”，等于该样本中所有数值由小到大排列后第75%的数字。

关于四分位数的应用，比较重要的就是绘制箱线图：

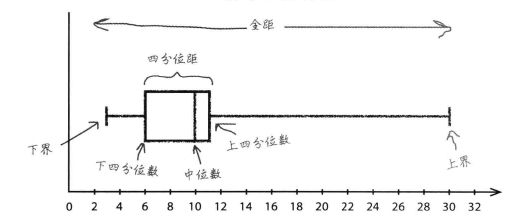
分位数除了四分位数外，还有十分位数，百分位数等。百分位数常用统计网站90%，95%，99%情况下的响应时间。

分布

均值、方差、标准差都是汇总统计量，可能会掩盖数据的真相。这是可以查看的数据的分布(distribution）。分布描述了各个值出现的频繁程度。

频数

频数指的是数据集中值出现的次数。给定一个序列t，频数计算如下：

hist = {}
for x in t:
	hist[x] = hist.get(x, 0) + 1

众数

分布中出现次数最多的值叫做众数(Mode)，即频数最大的那个值(可能多个)。众数是最适合描述典型值的汇总统计量。与均值、中位数一样，众数也有平均的含义

异常值

远离众数的值叫异常值(outlier），即频数最小的那个值(可能多个)。异常值可能是采集和处理数据过程中的错误导致的。

极差

极差(Range)为一组数据的最大值和最小值之差。极差的计算较简单，但是它只考虑了数据中的最大值和最小值，而忽略了全部观察值之间的差异

变异系数

变异系数(Coefficient of Variation (CV))又叫相对标准差（RSD），变异系数CV是原始数据标准差与原始数据平均数的比。标准差只能度量一组数据对其均值的偏离程度，CV用来来衡量不同总体数据的相对分散程度更合理。

概率质量函数

概率质量函数（probability mass function，简写为pmf）是离散随机变量在各特定取值上的概率。属于离散分布。

把上面计算频数改成计算概率，即频数除以样本数量n，得到值与概率映射即为概率质量函数。

n = float(len(t))
fpm = {}
for x, freq in hist.items();
	pmf[x] = freq/n

上面内容的思维导图：

参考

• 《统计思维》
• 揭开描述统计的神秘面纱